迷宫炸墙与迪杰斯特拉算法

10 August 2019 »数据结构与算法

问题描述
解决方案
总结

问题描述

这是上周面试的一道算法题：

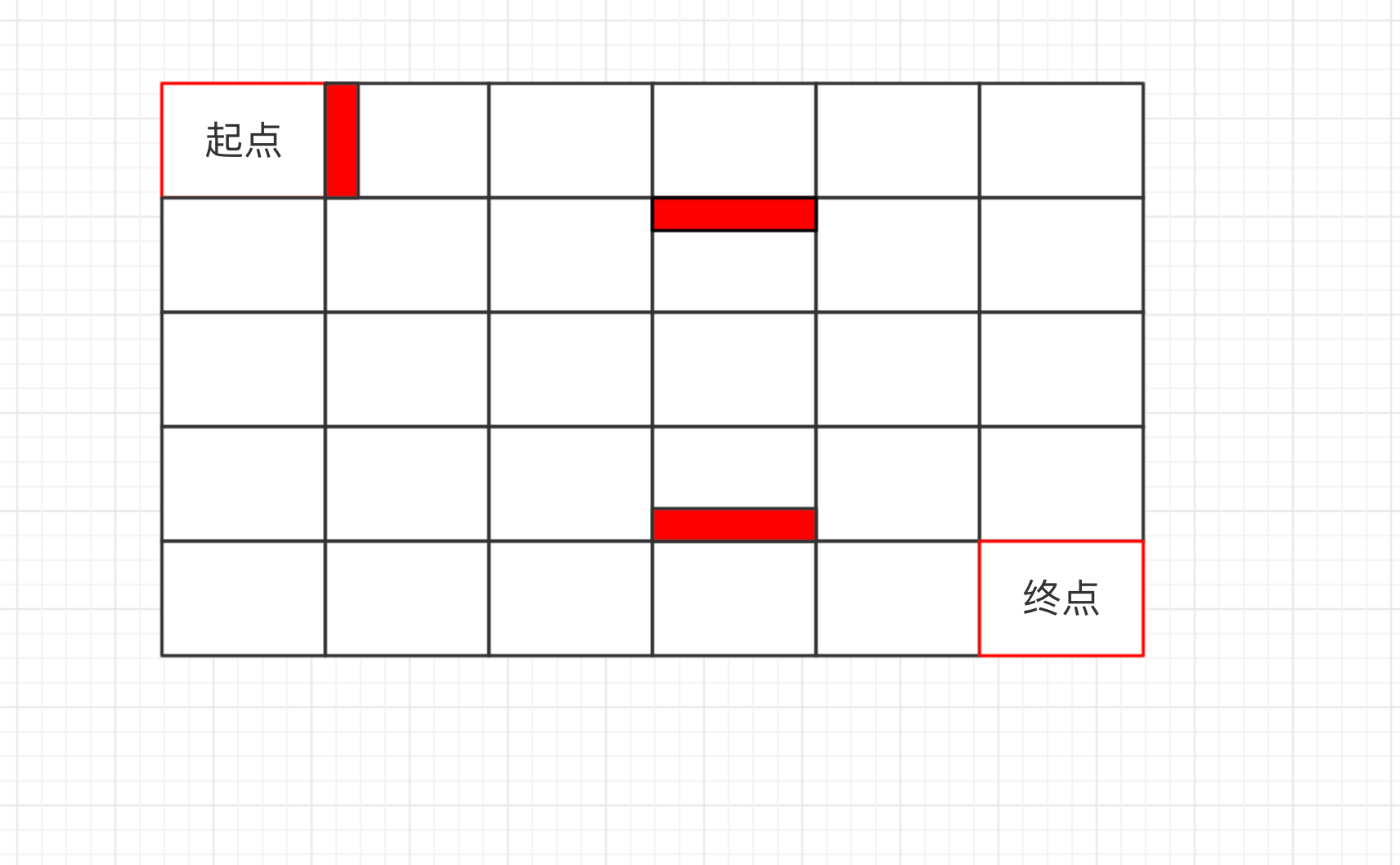
从起始点移动到终点
每移动一格所花费的时间为1，可以上下左右移动
格子之间可能存在墙，如果炸墙的话，那么时间花费为X（当时给的例子是3）
求从起点到终点花费的最短时间这题起初我以为是简单的动态规划可以解决，后来面试官说动态规划做不了，然后我说用DFS，DFS又确实太慢了。

最后没有做出来。回来想了一下，面试官应该是想我用迪杰斯特拉算法做。

解决方案

迪杰斯特拉是用来在图中求两个点之间的最短路径的算法。算法思想类似贪心，具体描述可以google一下。其主要用于求两个点之间的最短路径，而不适用于求所有点的最短路径，这主要是因为它每次只跟新了到起始

点的最短路径，而要想求所有点的最短路径，有更好的算法-弗洛伊德算法。

代码：

// 为了简化，这里就只给出一个入参，path表示初始的时候各个点的距离
//例如path[0][1] 表示第0个格子到第1个格子的最短距离，如果没有墙那么就是1，如果有墙那么就是3
// 非相邻的格子之间的距离都是Integer.MAX_VALUE
public int findMinTime(int[][] path){
	int start = 0; // 起始点,
	int end = path.length; // 终点
	Set<Integer> set = new HashSet<>();
	set.add(start);
	while(start.size() < end){
		int minTime = Integer.MAX_VALUE;
		int minPoint = 0;
		for(Integer index : set){
			if(index%path[0].length > 0 && !set.contains(index - 1) && path[index - 1][index] < minTime){
				minPoint = index - 1;
				minTime = path[index - 1][index];
			}
			if(index%path[0].length < path[0].length && !set.contains(index + 1) && path[index][index + 1] < minTime){
				minPoint = index + 1;
				minTime = path[index][index + 1];
			}
			if(index > path[0].length && !set.contains(index - path[0].length) && path[index - path[0].length][index] < minTime){
				minPoint = index - path[0].length;
				minTime = path[index - path[0].length][index];
			}
			if(index < end - path[0].length && !set.contains(index + path[0].length) && path[index][index + path[0].length] < minTime){
				minPoint = index + path[0].length;
				minTime = path[index][index + path[0].length];
			}
		}
		set.add(minPoint);
		// 更新路径
		for(int i = 0; i < path.length; i ++){
        	if(path[0][i] < path[0][minPoint] + path[minPoint][i]){
        		path[0][i] = path[0][minPoint] + path[minPoint][i]
        	}
		}
	}
	return path[start][end - 1];
}

总结

少壮不努力，老大要失业。