动态规划
»数据结构与算法目录:
适用求解问题
动态规划适用于求解最优解问题,通过将原问题分解为子问题,从而求解。与分冶法不同的是,分冶法是将大问题分解为互不相交的子问题,递归的求解子问题再将他们的解组合起来,求出原问题的解。而动态规划应用于子问题重叠的情况,即不同的子问题具有公共子子问题的情况。例如:求钢条分割、最长公共子序列等。
最优子结构:如果一个问题的最优解包含其子问题的最优解,我们就称此问题具有最优子结构。
重叠子问题:如果算法反复求解相同的子问题,我们就称为问题具有重叠子问题,例如爬楼梯,求解n层的时候需要求解n-1和n-2,求解n-1层的时候也需要求解n-2。
解题步骤
- 刻画一个最优解的特征。
- 递归的定义最优解的值。
- 计算最优解的值,通常采用自底向上的方法,也可以采用自顶向下带备忘的方法。
- 利用计算的信息构造一个最优解。
通常如果确定一个问题属于动态规划问题,那么关键点就需要去将问题分解为子问题的最优解结构。
案例
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。 问总共有多少条不同的路径?
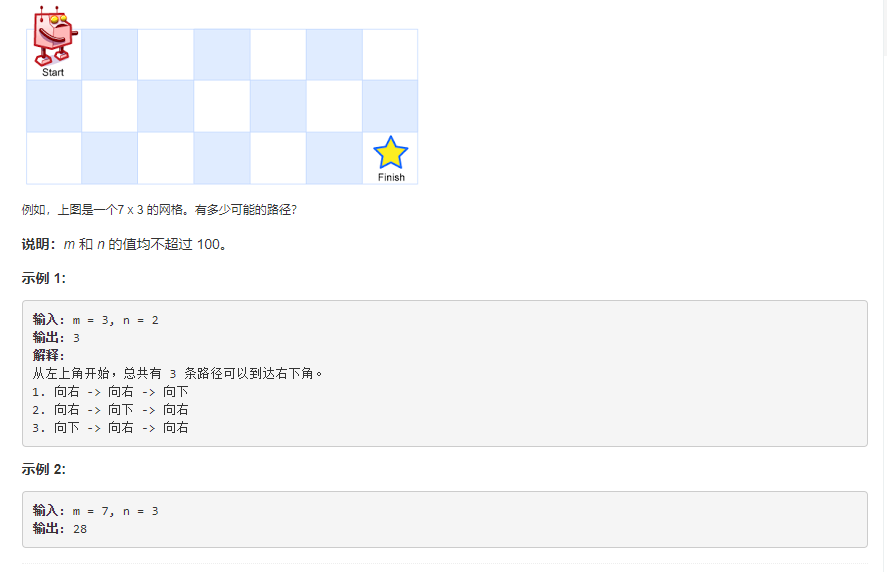
机器人每次有两种选择,向右或者向下,走完之后问题的规模就变小了,可以利用递归来做,但是会出现重复的子子问题,例如m = 5,n = 4
向右走 那么问题变成求m = 4, n = 4的情况 向下走,问题变成求m = 5, n = 3的情况 即path[5][4] = path[4][4] + path[5][3],但是可以发现这两种子问题都需要求path[4][3]等等 ,那么就可以用一种备忘的递归方法,记录下每次求的path,下一次需要的时候直接拿,不需要再重复计算。 或者采用自底向上的方法,先求出最小规模的问题,然后向上求解
/**
* 找出从左上角到右下角的路径,只能向右或向下
* 思路:每次都有两种情况向右或者向下,向右的话就变成m-1 n,向下的话就变成m n-1
* @param m
* @param n
* @return
*/
public int uniquePaths(int m, int n) {
// 记录规模为m n 的路径数
int[][] path = new int[m + 1][n + 1];
for (int i = 1;i<=m;i++){
path[i][1] = 1;
}
for (int i = 1; i <=n; i ++){
path[1][i] = 1;
}
for (int i = 2; i <=n; i ++){
for (int j = 2; j <= m; j ++){
path[j][i] = path[j-1][i] + path[j][i-1];
}
}
return path[m][n];
}
很多时候需要将动态规划,分冶区分开,要先确定一个问题到底需不需要用动态规划来做,如果一个问题本身就不需要用到动态规划,而你却用动态规划那么会耗费很多时间还做不出来。